
최근 경제적 소득수준의 증가로 인한 사치품 소비는 꾸준히 증가하고 있죠. 이에 따른 개인의 자산배분·소비·은퇴 문제와 이원화된 소비 행태 및 그에 따른 경제적 효용을 고려하는 것은 변화된 시대의 필수적 요소입니다. 또한 은퇴 시기에 있어 개인의 전 생애에 걸친 노동 수입과 지출 등을 주기별로 산출하는 것은 100세 시대의 장기적 자산관리의 중요한 요소로 작용하는데요.
UNIST 경영과학부 장현진 교수는 Imperial College London(ICL)의 교수진과 공동으로 소비의 이질성(기본소비 vs. 사치소비)에 대한 새로운 형태의 소비 효용함수를 연구했습니다. 공동 연구팀은 이를 토대로 개인의 전 생애에 걸친 자산배분, 소비 및 은퇴 시기에 대한 합리적 의사결정의 기준을 마련했습니다.
변화된 소비행태와 노동활동의 변동 주기를 현실적으로 가정하는 것은 안정적 자산관리를 위한 의사결정에 필수적 요소입니다. 하지만 이러한 가정들은 최적 자산배분, 소비 및 은퇴 모델 설립과정에서 제한 요소로 작용하게 되는데요. 이는 선택의 효용을 극대화하는 확률 최적화 문제(stochastic control problem)와 이에 대응되는 변동 부등식(variational inequality)을 도출하는 과정이 복잡해져 이론적으로 현상을 구현하는데 어려움을 증가시킵니다.
공동 연구팀은 이러한 비정상적 최적화 문제를 해결하기 위한 새로운 방법론적 접근 제시했습니다. 이원화된 소비의 비동조적 효용함수의 볼록화(convexification)인데요. 비동조적 소비효용함수는 볼록화 하더라도 주어진 결과에 영향을 미치지 않음을 이론적으로 증명함으로써 최적화 문제를 정의할 수 있었습니다. 또한 주어진 최적화 문제를 은퇴 전과 후로 분리해 보다 단순한 형태의 문제로 변환시켰습니다. 이러한 접근법은 주어진 문제의 복잡도를 현저히 감소시켜 이론적으로 다양한 시뮬레이션 구현을 가능하게 했습니다.
이번 연구의 시뮬레이션에 따르면 평균적인 경제 환경에 속해있는 중산층의 최적 은퇴시기는 30대 후반부터 40대 초반으로 나타났습니다. 이는 개인이 합리적 의사결정을 한다는 가정하에 기업이 설정해 놓은 60세 정년이 큰 의미가 없음을 보여 주는데요. 미국을 포함한 선진국들에서는 기업에서 공식적인 정년 기한을 두지 않습니다. 이는 노동자가 자발적 퇴사에 대한 합리적 선택을 하더라도 평균 정년은 적정수준으로 유지될 수 있다는 의미입니다. 이러한 정책은 노동자 입장에선 선택의 자유를, 기업 입장에선 정년설정으로 인한 불필요한 비용을 줄여 모두에게 유리한 결과를 가져올 수 있습니다.
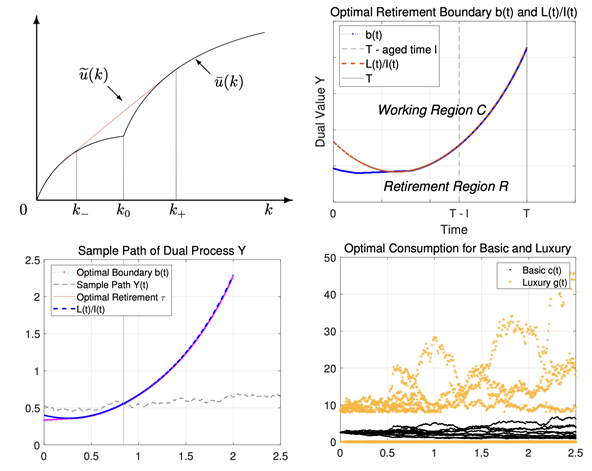
이번 연구를 통해 사치에 대한 높은 소비효용을 가진 중산층일수록 소비비중을 극도로 줄이는 ‘소비절벽’의 구간이 더 넓어진다는 것을 확인했습니다. 이들은 소비 대신 주식과 같은 자산투자의 비중을 높이려는 경향을 보였는데요. 이런 과도한 소비축소와 자산투자 등의 결과는 적절한 자산관리와 소비 확대를 위해 우리 정부가 어떠한 사회적 분위기와 정책 방향성을 나타내는지에 대한 지표가 됩니다.
장현진 경영과학부 교수는 이번 연구성과가 “경제학적 모델에 기반한 의사결정방법은 우리 사회에 이슈가 되고 있는 기업의 정년시기 적정성 평가 및 그에 대한 정책 결정에 보다 명확한 이론적 근거를 제시 할 수 있다”며 “우리나라 경제의 선순환 구조를 위한 중산층의 소비 확대 방안과 관련된 정책 결정에도 시사점을 줄 것이라 기대한다”고 밝혔습니다.
연구 결과는 '오퍼레이션즈 리서치(Operations Research)'에 2022년 10월 31일 온라인 게재됐습니다.
논문명: Optimal Investment, Heterogenous Consumption and Best Time for Retirement
#용어설명
1. 효용함수 (utility function)
경제학에서 개인이 어떤 선택을 함으로서 얻는 주관적 만족도을 효용이라 하고, 이 효용을 계량화한 함수
2. 확률최적화문제 (stochastic control problem)
확률적 움직임을 포함하는 시스템에서 어떤 주체행하는 선택의 효용을 극대화하는 의사결정의 방법을 다루는 문제
3. 변동 부등식(variational inequality)
확률최적화 문제를 확률미적분 및 동적계획법의 원리를 이용해 유도된 편미분항 등을 포함하는 특이형태의 부등식

